Evolution isn't over until you click stop

Why we need to run simulations out longer in Evolutionary Computation and Digital Evolution research

I thought I had this whole evolutionary computation thing down by now. After all, I've been evolving things inside the computer for 5 years. I've evolved robots. I've evolved digital critters. Heck, I've even studied how evolution works in complex digital fitness landscapes.

But nope. As always, evolution managed to surprise me. It wasn't a good surprise, either. It nearly led me to the wrong conclusion in one of my projects.

This time, I learned an important lesson about evolution: Evolution isn't over until you click stop.

"What does that mean?," you ask.

Well, let me tell you the story of how I came to this realization.

Short runs can lead to false conclusions

For the past year, I've been studying collective animal behavior using digital evolutionary models. I want to get at how and why animals work together in groups. For one of these projects, I was studying the effect of predator attack mode on the evolution of swarming behavior in a selfish herd. Everything was going smoothly. I had run my evolutionary simulations out to 1,200 generations -- the normal number of generations I run my simulations out to -- and I saw some clear evolutionary trends in the data, shown below.

[caption id="attachment_1653" align="aligncenter" width="723"]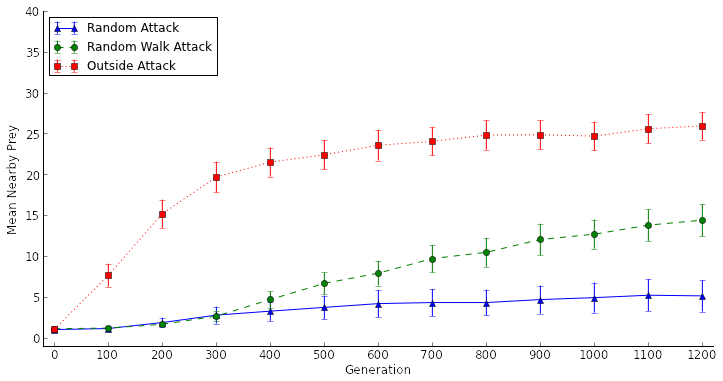 Artificial selection experiments at 1,200 generations. "Mean Nearby Prey" is a measure of how densely the prey are swarming, or if they are swarming at all. Error bars are 95% confidence intervals.[/caption]

From this data, I felt confident making three conclusions:

1. the Outside Attack treatment was strongly selecting for swarming behavior,
2. the Random Walk Attack treatment was weakly selecting for swarming behavior, and
3. the Random Attack treatment was not selecting for swarming behavior.

Perhaps the most controversial conclusion was the third one. It completely went against people's intuition of how the selfish herd theory works. Why wouldn't random attacks select for selfish herd behavior? There has to be an advantage to swarming, even with random attacks! But the data was pretty clear: Even at generation 1,200, the prey weren't swarming at all in the random attack treatment. Even the difference in "swarminess" between generations 1 and 1,200 in the Random Attack treatment wasn't statistically significant.

"Are you sure you ran the simulations out long enough?", one of my colleagues asked. I chuckled, feeling confident that 1,200 generations was more than enough to get a sense for the evolutionary trends in my model. And of course he'd ask that question. He's one of the researchers studying long-term evolutionary trends in the Long-term Experimental Evolution project. Nevertheless, I ran my experiments out for another 800 generations (for a total of 2,000 generations) to sate his curiosity.

[caption id="attachment_1654" align="aligncenter" width="719"]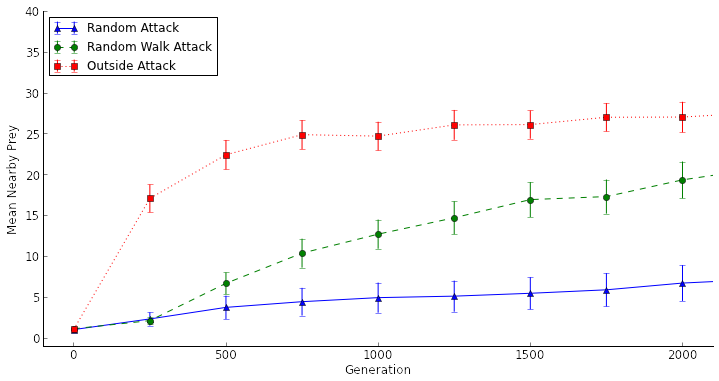 Artificial selection experiments at 2,000 generations. "Mean Nearby Prey" is a measure of how densely the prey are swarming, or if they are swarming at all. Error bars are 95% confidence intervals.[/caption]

That's when things got interesting. Suddenly that difference in "swarminess" between generations 1 and 2,000 in the Random Attack treatment was statistically significant. Suddenly it looked the beginnings of swarming behavior was evolving by generation 2,000 in the Random Attack treatment. My curiosity piqued, I ran the experiments out to 10,000 generations...

[caption id="attachment_1655" align="aligncenter" width="719"]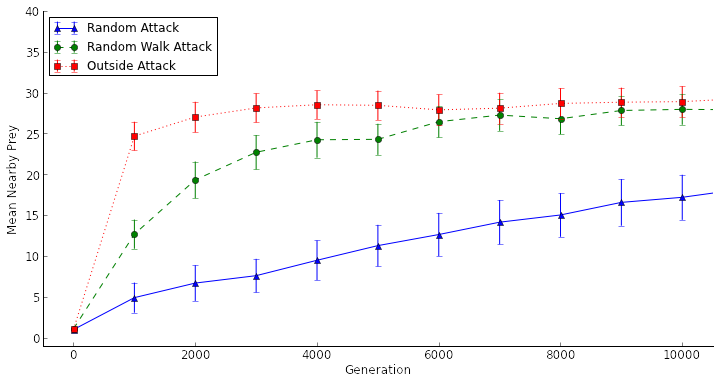 Artificial selection experiments at 10,000 generations. "Mean Nearby Prey" is a measure of how densely the prey are swarming, or if they are swarming at all. Error bars are 95% confidence intervals.[/caption]

WOAH!

What a difference a "few" generations can make!

If you look at generations 1,000 and 2,000 for the Random Attack treatment in the graph above, what originally looked a lot like a plateau was just the beginnings of a slow ascent toward swarming behavior. In fact, the difference between generations 1 and 2,000 look nothing like a plateau in this graph; it's pretty clear that the prey were beginning to swarm at that point. Rather than not selecting for swarming behavior at all, the Random Attack treatment merely exhibited a very weak selective pressure for swarming behavior. My original conclusion was wrong because I was ending my runs too early!

It was at this point that I learned...

Evolution can be surprisingly slow

[caption id="attachment_1656" align="aligncenter" width="731"]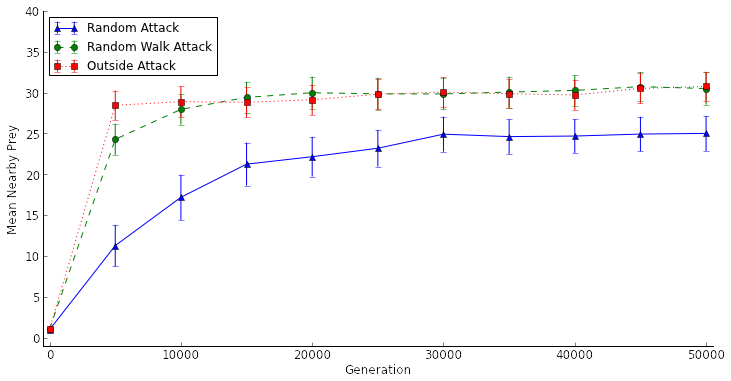 Artificial selection experiments at 50,000 generations. "Mean Nearby Prey" is a measure of how densely the prey are swarming, or if they are swarming at all. Error bars are 95% confidence intervals.[/caption]

It ended up taking about 20,000 generations for the prey in the Random Attack treatment to evolve visually noticeable swarming behavior, which is roughly 20x longer than the other two treatments. While I certainly wasn't wrong in claiming that the Random Walk Attack and Outside Attack treatments select much more strongly for swarming behavior, if I hadn't run the simulations out longer, I would have wrongly concluded that Random Attacks don't select for swarming behavior. I would have missed out on something much more interesting: that random attacks do indeed select for swarming behavior, but very weakly.

And that's how I learned my lesson: Evolution isn't over until you click stop. I was ending my runs too early and wasn't giving my digital critters enough time to figure out how to survive in their world.

What does this mean for Evolutionary Computation research?

I've read my fair share of Evolutionary Computation literature, and I'm not alone in cutting my runs short. I lost count of how many papers that report on simulations that only ran for 100 or 200 generations and claim that such and such evolutionary algorithm fails to find the optimal solution. Are 200 generations really enough to effectively explore the fitness landscape? If we're really so limited on time that we can only run 200 generations, is an evolutionary algorithm really the right algorithm to use?

The problem is even worse in projects that go unpublished. How many times have researchers run an evolutionary algorithm out for a couple hundred generations, didn't seen any progress, and called it quits and moved on to the next setup? I implore all Evolutionary Computation researchers to echo the words of my colleague to themselves the next time this situation is encountered: "Are you sure you ran the simulations out long enough?" You could be right on the edge of a really interesting discovery.

[caption id="attachment_1717" align="aligncenter" width="500"] If your evolutionary algorithm isn't performing as expected within a couple hundred generations, don't give up. You could be right on the edge of a really interesting discovery.[/caption]