Rethinking the population pyramid

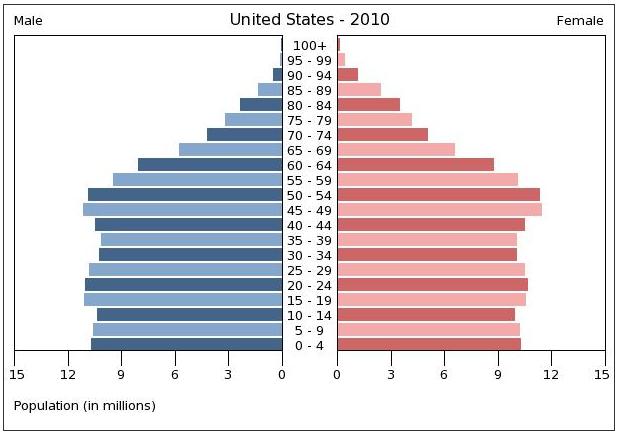
If you've ever browsed the U.S. Census population statistics pages, you've no doubt come across the famous population pyramid that they so frequently use to display the distribution of the U.S. population by age and gender.

I was reading up about population pyramids last weekend and ran across an interesting quote that caught my eye:

the use of a population pyramid is considered the best way to graphically illustrate the age and sex distribution of a given population.

Now, I'm no expert at displaying population statistics, but I was shocked at this claim. Could it really be true that population pyramids are considered the best method for displaying population distributions?

That line of thought ultimately led to the article below, where I raise three critiques of the population pyramid and present simpler and -- in my view -- more effective visualization methods.

For this article, I used the 2010 U.S. Census population statistics, which you can find here in a machine-readable format.

You can also find all of the code for these charts in my GitHub repository.

Problems with the population pyramid

1) Violates the standard expectation of having the causal variable on the x-axis

One of the most noticeable mistakes that the population pyramid makes is flipping the chart on its side to form a "pyramid" shape. I can only view this as an aesthetic flourish, since it violates one of the standard expectations of plotting: The causal variable should always be on the x-axis.

When it comes to plotting, the x-axis is typically reserved for the independent variable, i.e., a fixed setting that has some sort of effect on another variable. In contrast, the y-axis is reserved for the dependent variable, i.e., the variable that shows some effect from varying the independent variable.

The implication is that values on the x-axis cause some measurable effect on the values in the y-axis. This is why we always put the passage of time on the x-axis: it doesn't make sense to think of some other factor causing changes in the passage of time. (Until we discover time travel, anyway.)

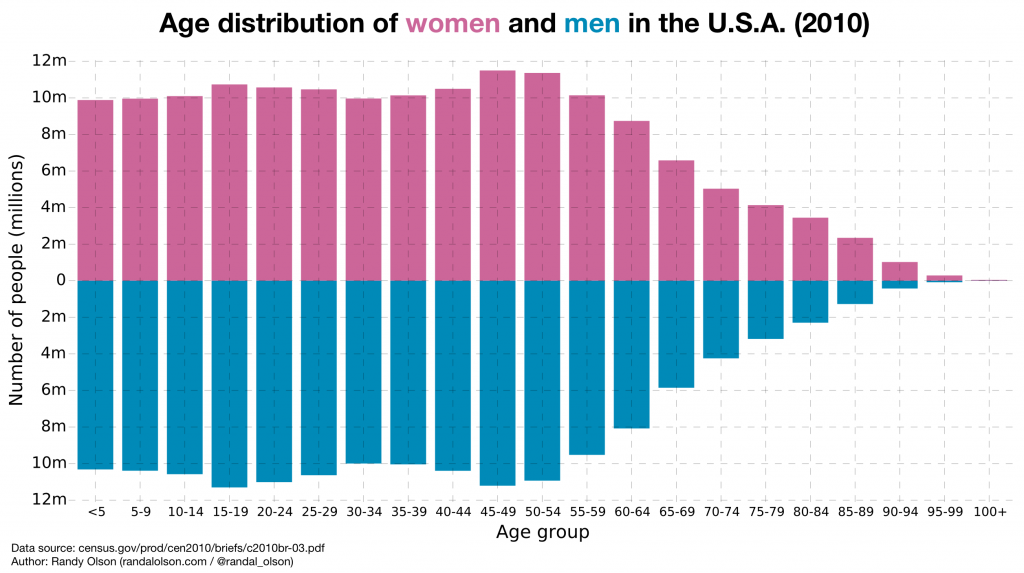
Since it doesn't make sense to think about a population's gender distributions having an effect on age -- and it makes far more sense to think about age having an effect on a population's gender distributions -- let's flip the axis of the pyramid so it's more in line with standard visualization practices.

Now we don't have to reorient ourselves every time we look at the population pyramid, since the data is displayed more naturally.

Ideally, the x-axis labels would be in between the "women" and "men" bars, but that was a bit tedious to pull off in my plotting software. Moving on...

2) Doesn't allow direct comparisons between the two categories

The second flaw with population pyramids is that they make it difficult to compare the age distributions of men and women.

For example, can you tell me at a glance if there's more men or women in the 25-29 age group? You'd have to look up the number of men and women in the 25-29 age group separately and make the comparison that way, when there's really no reason that the chart shouldn't be performing those comparisons for you.

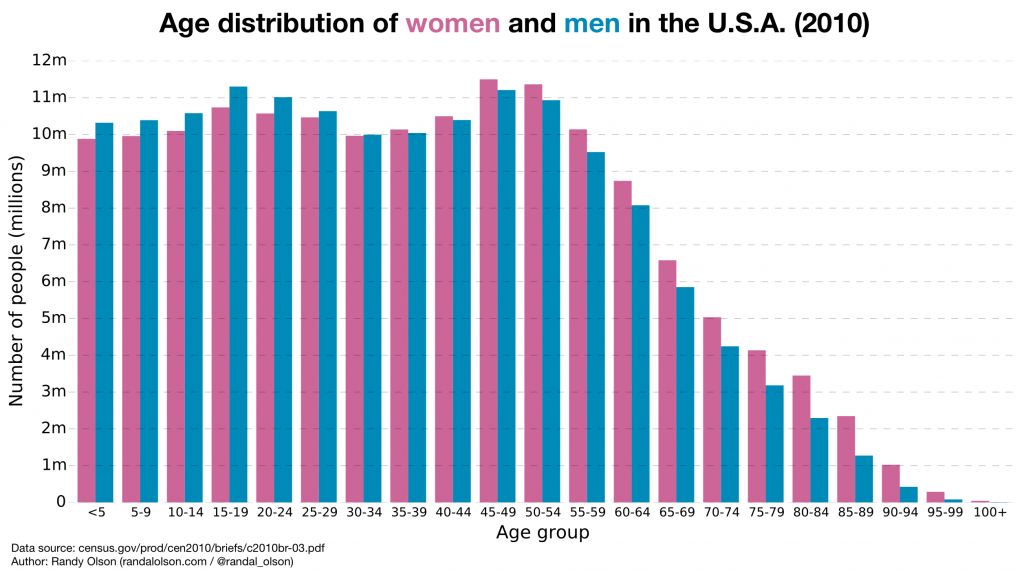
Let's rework the population pyramid to group the people by age, with separate bars for men and women.

Now we have the exact same benefits of the population pyramid, with the additional benefit of being able to immediately discern whether there are more women or men in each age group. Arguably, we can now perform the same comparison between age groups as well -- for example, are there more 50-54-year-old women than 30-34-year-old men? -- but those comparisons become difficult the further the age groups are from each other.

What's immediately apparent from this version of the population pyramid is:

1. There are more young men than young women in the U.S.,
2. we reach gender parity around age 30,
3. then men start dying out younger and leaving droves of widows behind starting at age 45.

There's some really interesting implications in that data for the evolution of human sex ratios, but I'll leave that for another time.

3) Relative trends between the categories are masked by displaying absolute values

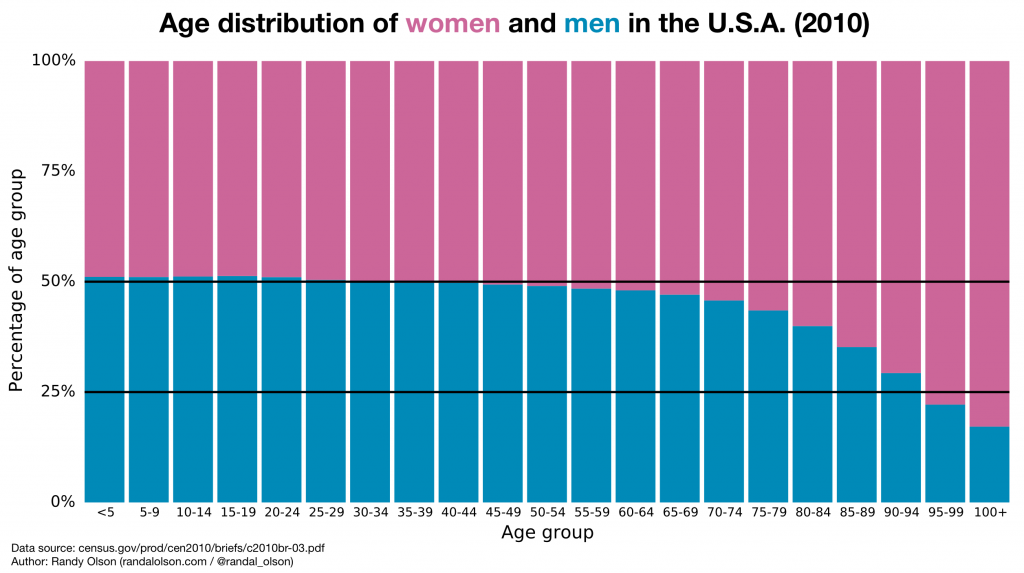
There's clearly an interesting trend going on in the age 45+ groups where there are more women than men. But what's going on with the M:F ratio, especially in the 90+ categories? It's incredibly difficult to tell because these trends are masked when we display absolute values.

If we're more interested in the relative trends between the two categories, we can drop the absolute values and instead show the percentage breakdown of the groups as I've done below.

Now those trends I discussed above become abundantly clear, and we see that roughly 75% of U.S. adults aged 90+ are women. Sorry, straight men: your wife is probably going to outlive you.

Of course, whether we would use this third chart solely depends on whether we care more about relative differences between the gender categories or the age distribution of the population. As with all charts, what data you should display depends on what story you want to tell with the data. In either case, I hope I've convinced you that the population pyramid -- as it's currently used -- is not quite ideal for telling either story.

Lessons learned

As with all of my long-winded articles critiquing a data visualization, I'll end with a brief summary of the main lessons we've learned.

1. The causal variable (e.g., time or a parameter you control in an experiment) should always go on the x-axis.
2. Group related data when within-group comparisons can be useful.
3. What chart you use and what data you display depends on the story you want to tell. Don't try to force a story out of the wrong chart.

Are there some other ways the population pyramid could be improved? Leave your suggestions in the comments.

If you liked what you saw in this post and want to learn more, check out my Python data visualization video course that I made in collaboration with O'Reilly. In just one hour, I will cover these topics and much more, which will provide you with a strong starting point for your career in data visualization.