Chess tournament games and Elo ratings
Published on May 24, 2014 by Dr. Randal S. Olson
chess match draw elo rating expert first-move advantage stalemate
6 min READ
Chess is by far one of my favorite games. Ever since Seth Kadish shared one of his visualizations of square utilization by chess masters, I've been wanting to follow up to see what else we can visualize about chess. A few months ago, Daniel Freeman from ChessGames.com generously opened his chess data set to me to analyze, which contains a huge collection of 675,000+ chess tournament games ranging all the way back to the 15th century. This will be the first in a series of blog posts exploring this data set. To begin, I was interested in Elo ratings and how they predict the outcome of chess games.
[caption id="attachment_4178" align="aligncenter" width="768"] Chess match: Bobby Fischer vs. Mikhail Tal (1960)[/caption]
Chess match: Bobby Fischer vs. Mikhail Tal (1960)[/caption]
The goal of the Elo rating system is to assign a numeric value that represents a player's chess skill. It's a fairly straightforward yet elegant rating system:
- All new players start at a relatively low Elo rating.
- If you beat someone, your Elo rating goes up and their rating goes down the same amount, and vice versa if you lose.
- The number of points your rating changes by is determined by the difference between you and your opponent's rating.
For example, if you have an Elo rating of 1600 and beat a 2200 rated player, your ratings are going to change a lot. But if you beat a 1000 rating player (as a 1600 rating player), your ratings won't change much.
Therefore, it's in your best interest to play against others around or above your current Elo rating. After dozens of games, you'll eventually arrive at an Elo rating that's representative of your chess skill.
Distributions of Elo ratings
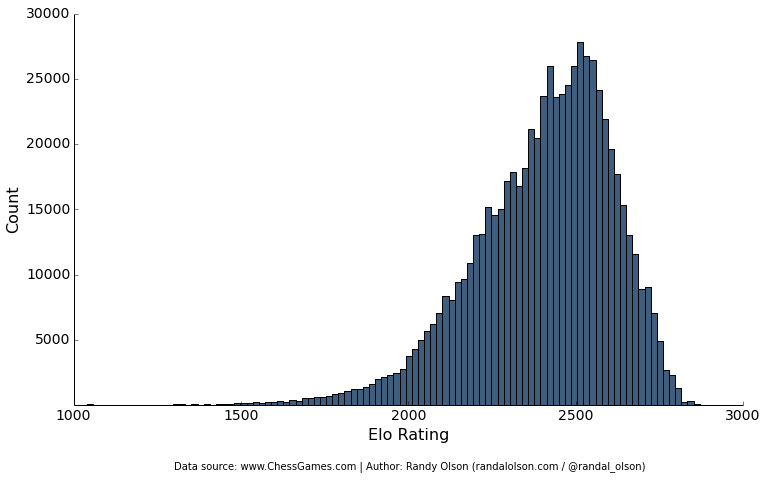
Let's start by jumping into the diagnostics. Since this is a data set of chess tournament games, most of the rated players have pretty high Elo ratings. The majority of the games I'll be analyzing were played by experts with a 2000+ Elo rating, many in the 2500 range. To give you a sense of what these ratings mean: Bobby Fischer's peak rating was 2785, and Garry Kasparov's was 2851. So we're analyzing games by some pretty talented chess players.
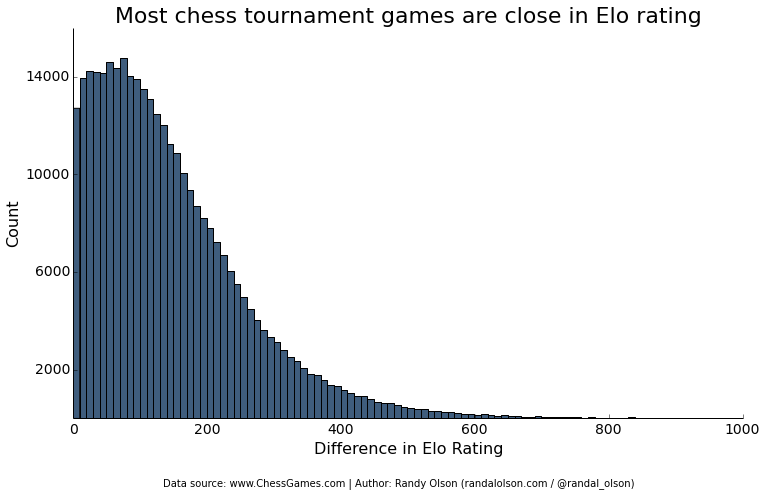
Another important factor to look at is the difference in Elo ratings between the two players in each game. Following the wise advice above, most of the chess tournament games were played between competitors with a fairly close Elo rating. This will be important to keep in mind later as I look at the effect of differences in Elo ratings.
Enough diagnostics. Let's get into the meat of the data.
Elo ratings tend to predict game outcome
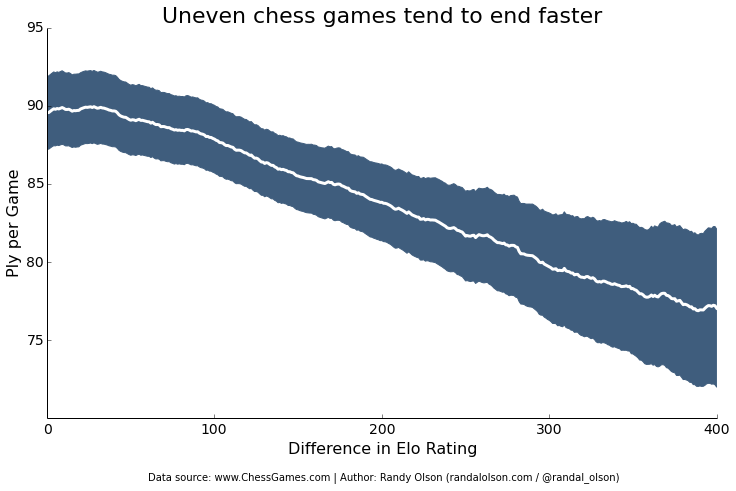
My experience with playing against higher-rated players is that the game always seems to end quickly with a checkmate. Sure enough, I'm not the only one to experience this: The higher the difference in Elo rating, the faster the game reaches its final conclusion. The typical game with evenly-matched competitors lasts about 90 plies (45 moves), whereas expert vs. rookie games tend to end in a mere 77 plies (38 moves).
Some of the shortest chess games end in a Fool's Mate, where Black checkmates White on her second move. I haven't been able to look if such a game happened in this data set, but it's unlikely because Fool's Mates typically only happen in rookie play. In contrast, the longest recorded chess game was between Ivan Nikolic and Goran Arsovic in 1989, who took a whopping 20 hours to play 269 moves that ended in a draw. Talk about dedication!
(Note: In all of the following plots, the white line is the mean and the shaded blue area is the 95% confidence interval.)
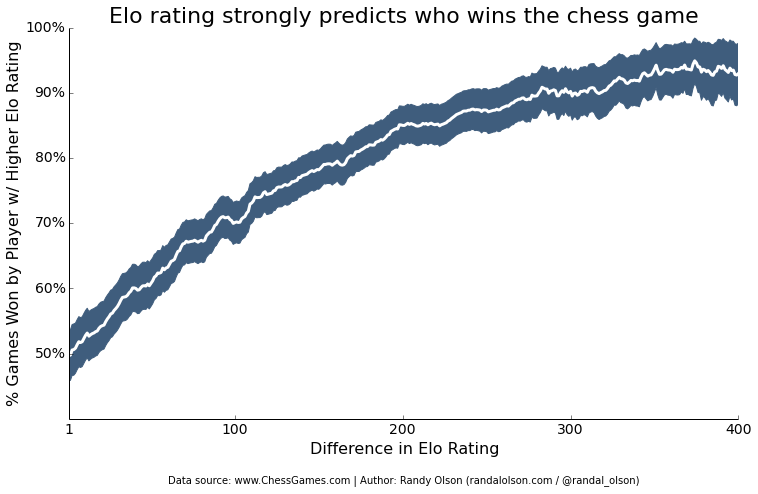
Furthermore, relative Elo ratings strongly predict who's going to win the game. Evenly-matched competitors have a 50/50 chance of winning, but the more uneven the match is, the more it swings in favor of the competitor with the higher Elo rating. I'd imagine the only reason this trend levels out at ~90% is because this data set contains games where a talented new player hasn't quite reached their proper Elo rating yet.
As an extreme case, 9-year-old Awonder Liang defeated GM Larry Kaufman in 2012 in a stunning performance that went straight into the world record books.
These findings are likely unsurprising for experienced chess players: Elo ratings tend to accurately predict the outcome of a game. For those who are newer to chess, just know this: If you're pitted against someone with a much higher Elo rating, you can expect a quick and decisive defeat.
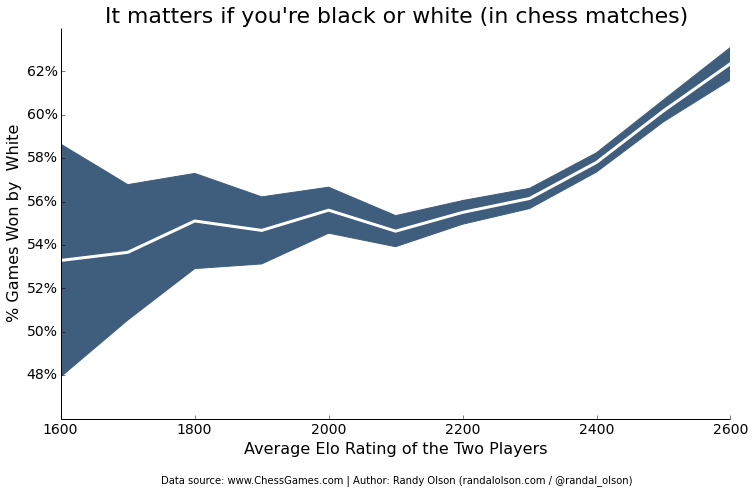
It matters if you're black or white
An often-cited problem with chess is the first-move advantage. Because the White player gets to move first, they get to set the stage for how the game will turn out -- if they know what they're doing. Sure enough, we see exactly that effect in this data set: Newer players with an Elo rating < 1800 tend to lose the first-move advantage and still only win 50% of the non-drawn games as White. Meanwhile, the first-move advantage becomes increasingly pronounced the more skilled the players are, where expert players win as much as 62% of their non-drawn games when playing as White.
Contrary to Michael Jackson's famous pop song, it matters if you're Black or White in chess. Newcomers, take note: Try to play as White as much as possible and learn to harness the first-move advantage.
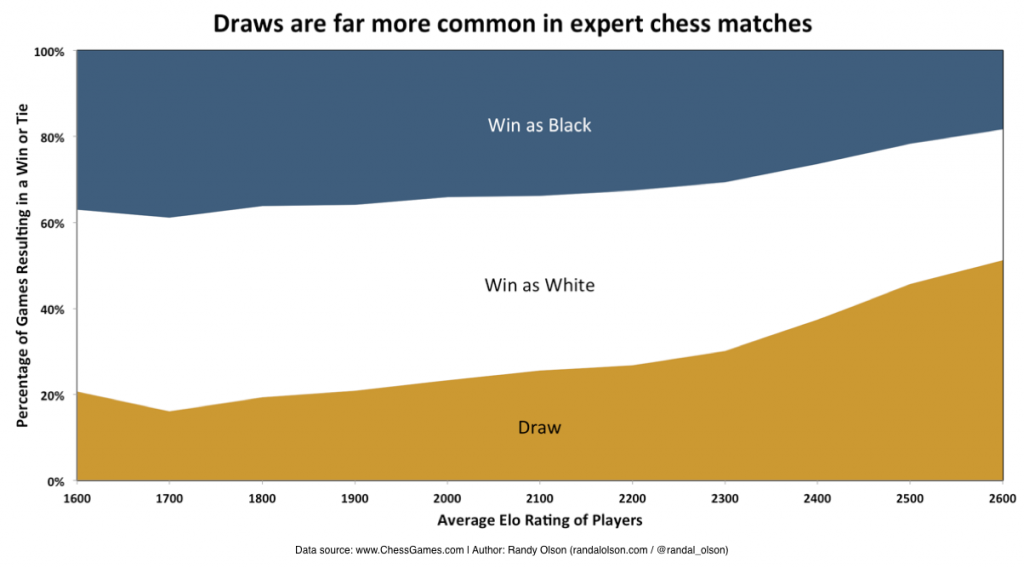
Draws are more common in expert games
Finally, I wanted to take a look at the breakdown of wins, losses, and ties by player skill. I've always heard that rookie chess games tend to be more decisive than expert games, but I'd never seen any data on it. The theory makes sense, of course: rookies tend to leave more openings than their more experienced counterparts, making it easier to close the game with a checkmate.
Sure enough, we see a dramatic rise in tie games from rookie (20% draws) to expert (50% draws) games. Your eyes aren't fooling you: Half of all expert chess games end in a draw. We also see the first-move advantage in this chart, where it becomes less and less common for players to win as Black in expert games. Several chess theoreticians even argue that in a perfectly played game, the best outcome for Black is a draw. Unsurprisingly, luring your opponent into a draw has become somewhat of an art as Black.
So there you have it. Elo ratings predict the outcome of a chess game in several ways. It'll be interesting to break Elo ratings down by year and see how they've evolved over time.
What else can we learn from this data set? Leave your suggestions (and why it'd be an interesting analysis) in the comments.